Conseils de calcul pour la détermination du coût du capital

Nous avons eu à lire les dix-huit évaluations faites par des banques et des experts indépendants sur neuf entreprises cotées, objets en mars et avril d’une d’offre publique, le plus souvent suivie d’une expropriation des actionnaires si le seuil de détention de 90 % était atteint. À l’exception d’une entreprise (Natixis), toutes ces offres portaient sur des valeurs du flottant comprises entre 2 et 95 M€. Cette étude nous a inspiré les quelques suggestions suivantes.
Le taux de l’argent sans risque
Pour aboutir à la formule bien connue de détermination du taux de rentabilité à exiger d’un actif, qui est rF + β x (E(rM)- rF), à un moment donné dans la démonstration, il est nécessaire de prendre pour l’écart-type du taux de rentabilité de l’actif sans risque le chiffre de 0 (sinon on n’aboutit pas à cette formule, mais à une autre plus complexe). Ce qui est logique, car si un actif sans risque est sans risque, c’est que sa rentabilité est certaine, et que donc l’écart-type de sa rentabilité est nul. Et si cette situation n’est pas vérifiée, c’est que l’actif sans risque n’est pas dénué de risque, autrement dit qu’il n’est pas un actif sans risque !
Qu’appelle-t-on alors un actif sans risque ? Les pères fondateurs du MEDAF se sont bien gardés de le définir autrement que par sa caractéristique congénitale : l’écart-type de sa rentabilité est nul. Si tout le monde est d’accord pour prendre le taux de rentabilité d’un instrument financier émis par un État solvable pour éviter le risque de crédit, les praticiens retiennent souvent, mais à tort à notre avis, une obligation à 10 ans, sous un double prétexte : c’est souvent la plus liquide des obligations d’État et la référence. Sa durée de vie donne l’impression (fausse en réalité) de correspondre grosso-modo à celle de la duration des flux de l’action à évaluer (qui est en fait infinie contrairement à celle d’une obligation). Mais c’est oublier que sur une période de 10 ans, la rentabilité des obligations d’État est tout sauf stable, ce que le MEDAF présuppose et requiert. On serait bien en peine dans ce graphique, qui retrace depuis 1972 les taux d’intérêt actuariel d’une obligation d’État à 10 ans (OAT), de trouver une seule période de 10 ans de stabilité, et donc un écart-type nul :
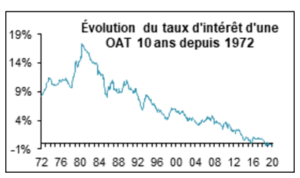
Il est donc plus raisonnable et correct de prendre comme taux de l’argent sans risque le taux actuariel d’un bon du Trésor à court terme, par exemple à un mois, qui est exempt de cette tare : sa rentabilité actuarielle en fin de période sera bien celle annoncée initialement, sa courte durée garantissant un écart-type nul des rentabilités de cet actif sans risque comme il se doit.
Signalons que dans notre échantillon, trois évaluateurs sur dix-huit ont décidé de prendre 0 % quand le taux de l’argent sans risque qu’ils avaient choisi était négatif, un peu comme les banques qui prennent Euribor à 0 % pour calculer les intérêts que leur doivent leurs clients. À notre avis et à notre connaissance, rien ne justifie cette position arbitraire en matière d’évaluation.

Pour chaque dossier la première ligne correspond au travail du présentateur et la seconde à celui de l’expert indépendant.
Notre lecteur, comme nous, ne manquera pas d’être frappé par la dispersion des moyennes prises en compte : du spot à 10 ans.
Le coefficient β
Dans notre petit échantillon, que le β soit celui des capitaux propres ou de l’actif économique (désendetté), les durées de son calcul sont très diverses : près de la moitié des évaluateurs ne donnent pas cette information ; quant aux autres, ils répartissent à peu près également entre 1, 2, 3 et 5 ans.
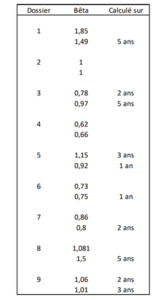
Nous ne saurions trop vous conseiller de retenir une durée de 3 ans, non pour jouer la moyenne, mais parce que des chercheurs ont démontré que c’était la durée la plus fiable[1]; plus longue, on prend le risque que l’entreprise ait bien changé et que son β actuel reflète plus un passé révolu que la situation actuelle ; plus courte, et le calcul risque de ne pas avoir assez de points pour être significatif, d’autant que les coefficients β sont rarement calculés quotidiennement (ce qui nous semble pourtant le plus correct), mais plutôt hebdomadairement, voire mensuellement.
La prime de risque
C’est un piège à tous les niveaux, comme en témoigne la très grande dispersion des primes utilisées dans les 18 évaluations, qui pourtant se concentrent sur une période de seulement 2 mois : de 5,5 % à 10,5 %, quasiment du simple au double, ce qui laisse songeur !
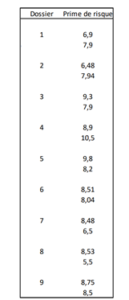
Commençons par le piège le plus redoutable car le plus inaperçu. Si la prime de risque est égale à (E(rM)- rF), elle est rarement calculée par les évaluateurs comme une soustraction entre l’espérance de rentabilité du marché et le taux de l’argent, mais est le plus souvent une donnée externe, fournie par un tiers, et c’est là que se trouve le piège, dans lequel heureusement tous les évaluateurs ne tombent pas.
En effet, par définition rF = rF (nous espérons que vous nous suivez !), autrement dit le taux de l’argent sans risque pris dans le calcul de la prime de risque doit être le même que celui correspondant à la première composante du taux de rentabilité à exiger dans la formule : rF + β x (E(rM)- rF ). Sinon, il y a un problème. Et nous avons frémi devant des cas où la prime est calculée sur des données américaines tandis que le taux de l’argent sans risque vient des OAT 10 ans. Merci la cohérence ! Nous avons vu d’autres cas où, comme dit l’épouse de l’un d’entre nous, l’évaluateur a visiblement fait une « glisse légère » en ne précisant pas ses sources, pour que le problème ne se voit pas trop.
Nous vous conseillons, plutôt que de demander à un tiers fournisseur son estimation de la prime de risque, de lui demander son estimation du taux de rentabilité espérée sur le marché, c’est-à-dire le E(rM). Ainsi vous éviterez de tomber dans ce piège.
De la même façon, nous vous conseillons d’éviter de prendre des primes historiques, c’est-à-dire calculées sur une moyenne des données passées plus ou moins longue, pour ne prendre que des primes de risque anticipées, c’est-à-dire ressortant implicitement des cours actuels. Ainsi, quand vous allez acheter des dollars par exemple, peu vous chaut le cours moyen du dollar à 5 ou 10 ans. Tout ce qui compte, à juste titre, est le cours du jour, car c’est à ce prix-là que vous pouvez les acheter. Il en est de même en évaluation. On peut prendre des moyennes à court terme (jusqu’à 3 mois) si on a peur de la volatilité, mais guère au-delà, nous semble-t-il.
Dans notre échantillon, huit évaluateurs prennent des moyennes de 3 mois au plus ou des estimations spot, un prend une prime historique calculée sur 119 ans (!), un autre sur 10 ans, un sur 2 ans, un autre sur 6 mois. Six évaluateurs ne précisent rien.
Les primes de risque spécifiques
Quelle hérésie ! En effet, en finance, seul le risque de marché est rémunéré. Le risque spécifique, pouvant s’éliminer sans coût pour l’investisseur par la diversification de son portefeuille, n’est pas rémunéré. Dès lors, il n’y a pas lieu d’ajouter au taux de rentabilité, déterminé par la formule du MEDAF vue plus haut, de prime pour des risques spécifiques. C’est antinomique.
Les primes de liquidité ou d’illiquidité
Si l’ajout d’une prime spécifique au taux de rentabilité à exiger d’un actif est incorrect, la prise en compte d’une prime de liquidité ou d’illiquidité peut se justifier pour des valeurs où la liquidité est faible, à la fois parce qu’elle correspond à une réalité que l’on peut observer, et parce que ses fondements théoriques sont assez bien assis. Ainsi, le modèle de Fama-French7 de 1992, qui est le seul modèle qui puisse pratiquement rivaliser avec le MEDAF, fait dépendre le taux de rentabilité à exiger d’un actif, de la rentabilité du marché comme pour le MEDAF, et de l’écart de rentabilité entre les grosses capitalisations et les petites, et donc de cet aspect liquidité.
Mais la prise en compte de la liquidité ne doit pas se faire par l’ajout d’une prime de liquidité à l’équation de la droite de marché, car ceci est méthodologiquement incorrect.
Si l’on veut faire dépendre la rentabilité requise de deux paramètres, le taux de rentabilité du marché et la liquidité, comme cela est fait dans le modèle de Fama-French, on ne calcule pas déjà la rentabilité à exiger d’une action en fonction de la rentabilité du marché et de son b (l’équation de la droite de marché) ; pour ensuite ajouter une prime de liquidité, qui a été calculée par ailleurs, le plus souvent à une autre époque et dans d’autres conditions de marché. Non. On calcule directement la rentabilité à exiger d’une action en fonction conjointe des deux paramètres rentabilité du marché et liquidité.
Associés en Finance publie depuis des années à la fois une droite de marché (un seul facteur explicatif à la rentabilité exigée, la rentabilité du marché par le biais du b de l’action) et un plan de marché (deux facteurs explicatifs à la rentabilité exigée, la rentabilité du marché et la liquidité).
Ainsi, fin avril, l’équation de la droite de marché Associés en Finance était de :
k = – 0,6 % + β × 8,6 %
Et celle du plan de marché de :
k = 0,3 % + β × 6,0 % + λ × 0,9 %, avec le coefficient λ qui est à la liquidité ce que le coefficient β est au risque de marché.
Comme notre lecteur peut le constater, la seconde équation n’est pas simplement la première avec l’ajout en fin de formule d’un supplément de rentabilité à exiger pour tenir compte de la liquidité de l’action. Non. C’est une autre formule avec des paramètres différents.
Mais il y a un cas de figure où l’usage d’une prime de liquidité nous paraît tout à fait inadmissible, c’est celui du retrait de cote (le squeeze out des Anglo-Saxons). Car il s’agit d’être logique. Si l’actionnaire majoritaire fait une proposition aux actionnaires minoritaires de leur racheter en numéraire leur actions, offre pouvant devenir contraignante et se transformer en expropriation si le seuil de 90 % est dépassé, où est l’illiquidité qui justifierait une décote, puisque l’offre est en numéraire ? C’est un peu comme si au moment d’exproprier votre terrain qui se trouve sur le passage d’une autoroute à construire, on appliquait une décote à sa valeur, sous prétexte que, maintenant, votre terrain est devenu non constructible, et vaut donc moins cher !
En revanche, pour la cession d’un bloc, pour une introduction en Bourse, on pourrait tout à fait comprendre qu’une prime d’illiquidité soit ajoutée au taux d’actualisation. C’est bien d’ailleurs ce que l’on observe avec la décote d’introduction en Bourse, ou celle extériorisée par les reclassements de blocs (ainsi Engie a cédé il y a quelques semaines 10% de GTT pour 250 M€, avec une décote de 7,1% par rapport au cours).
Les primes de taille
Elles sont à nos yeux spontanément suspectes, car elles ne sont pas clairement définies. Elles s’apparentent souvent à des primes spécifiques dont nous avons dit tout le mal que nous en pensions plus haut ; et parfois elles recoupent les primes de liquidité, et donc conduisent tout droit à compter deux fois la même chose quand elles sont recevables.
Comme le montre le tableau suivant, un coefficient β correctement calculé montre déjà une corrélation inverse avec la capitalisation boursière :
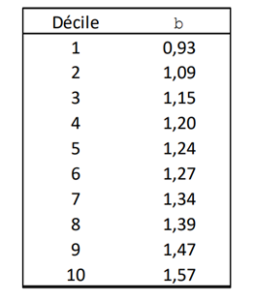
La première colonne range les capitalisations boursières par déciles décroissants, les petites capitalisations sont donc dans le bas du tableau. On constate clairement dans cette recherche de[2]8 , qui couvre 68 années, que plus une entreprise est petite, plus son coefficient β est élevé. Autrement dit, si on calcule correctement le coefficient β d’une petite capitalisation par régression linéaire contre l’indice, un effet taille est déjà inclus dans le taux d’actualisation. Ajouter une prime de taille conduit donc à compter deux fois le même effet, c’est une fois de trop ! Toutefois, les trois chercheurs précités ont mis en évidence que les β des petites capitalisations étaient trop souvent calculés avec un biais les minorant. En effet, contrairement aux plus grandes capitalisations, la vitesse d’ajustement des petites capitalisations aux fluctuations du marché est plus lente, à cause de leur liquidité moindre. En calculant les coefficients β en prenant en compte cette inertie, les trois chercheurs ont obtenu le tableau suivant :
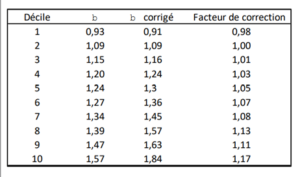
On voit ainsi que pour les plus petites capitalisations boursières du dernier décile, l’augmentation du coefficient b est de 17 %. En prenant la prime de risque moyenne de notre échantillon de 8,2 %, l’impact de cette correction du b conduit à ajouter environ 1,5 % au taux d’actualisation, et non pas les 3,2 % en moyenne qu’ajoutent ceux des évaluateurs qui prennent en compte une prime de taille.
Les primes de contrôle
Terminons avec une considération plus générale, qui est celle de la prime que représente le prix proposé dans l’offre par rapport au cours spot avant l’annonce de l’offre, ou par rapport à une moyenne des cours calculée sur un ou plusieurs mois. Dans notre échantillon de neuf transactions, les primes spots s’étagent entre 8 % à 61 %, et pour celles calculées à un mois, entre 11 % et 57 %.
Même si la moyenne de ces primes est de 24 % et 26 % respectivement, la prime n’est que la résultante du résultat de l’évaluation par rapport au cours coté, et n’en est pas la source, comme trop souvent nous avons entendu des chefs d’entreprise nous le dire, en estimant qu’il suffisait de rajouter une prime de l’ordre de 25 % au dernier cours de Bourse pour trouver le bon prix pour exproprier les minoritaires. Non, la charrue ne se met pas avant les bœufs !
[1] N. Groenewold., P. Fraser, « Forecasting beta: how does the “five-year rule of thumb” do? », Journal of Business & Accounting septembre-octobre 2000, vol. 27, nos 7-8, p. 953 à 982.
[2] R. Ibbotson, P. Kaplan et J. Peterson, 1997, « Estimates of Small Stock Betas are Much Too Low », Journal of Portfolio Management, juillet, vol. 23, n°4, p. 104 à 111.
Cet article a été publié dans le n°189 de la Lettre Vernimmen. Il est repris par Vox-Fi avec due autorisation. Cet article a également été publié sur Vox-Fi le 6 juillet 2021.








