Quand la machine reconnaît les visages

Le livre compte à coup sûr parmi les meilleurs sur l’intelligence artificielle (IA) : Pedro Domingos, The Master Algorithm. How the Quest for the Ultimate Learning Machine Will Remake Our World, 2015, non traduit malheureusement. Bill Gates en dit ceci : « Pedro Domingos lève le voile, de l’intérieur, sur les machines à apprendre qui alimentent Google, Amazon et votre smartphone. Il discute de ce que cela signifiera pour les affaires, la science et la société. Si le data-isme est la philosophie d’aujourd’hui, ce livre en est la bible. »
De fait, Domingos détaille les différentes approches et conceptions, parfois rivales, qui expliquent les fantastiques progrès dans ce domaine. Il le fait à l’américaine, dans un langage simple, anecdotes et réflexions plus profondes entremêlées.
Ici, sur Youtube et dans le cadre des conférences TED, on trouvera le topo fait par l’auteur sur le sujet.
Vox-Fi propose à ses lecteurs un extrait traduit du chapitre 8, donnant un aperçu pédagogique simple sur la reconnaissance faciale via les machines.
Un visage ne comporte qu’une cinquantaine de muscles, donc cinquante nombres devraient suffire à décrire toutes les expressions possibles. La forme des yeux, du nez, de la bouche, etc. – les caractéristiques qui vous permettent de distinguer une personne d’une autre – ne devrait pas non plus nécessiter plus que quelques dizaines de chiffres. Après tout, avec seulement dix choix pour chaque trait du visage, un artiste de la police peut réaliser le portrait-robot d’un suspect suffisamment bon pour le reconnaître. Vous pouvez ajouter quelques nombres supplémentaires pour spécifier l’éclairage et la pose, et c’est à peu près tout. Donc, si vous me donnez une centaine de chiffres, cela devrait me suffire pour recréer l’image d’un visage. Ainsi, le cerveau de Robby [Robby est le nom du robot que nous voulons éduquer à reconnaitre les visages] devrait être capable de prendre l’image d’un visage et de la réduire rapidement aux cent chiffres qui comptent vraiment.
Les apprentis-machines appellent ce processus « réduction de la dimensionnalité » car il réduit un grand nombre de dimensions visibles (les pixels) à quelques dimensions implicites (expression, traits du visage). La réduction de la dimensionnalité est essentielle pour faire face aux données massives, comme celles qui parviennent par vos sens à chaque seconde. Une image vaut peut-être mille mots, mais elle est aussi un million de fois plus coûteuse à traiter et à mémoriser. Pourtant, votre cortex visuel parvient à réduire ces données à une quantité gérable d’informations, suffisante pour naviguer dans le monde, reconnaître les personnes et les objets et se souvenir de ce que vous avez vu. C’est l’un des grands miracles de la cognition et c’est tellement naturel que vous n’en êtes même pas conscient.
Lorsque vous disposez des livres sur une étagère de manière à ce que les livres traitant de sujets similaires soient proches les uns des autres, vous effectuez une sorte de réduction de la dimensionnalité, du vaste espace des sujets à l’étagère unidimensionnelle. Il est inévitable que certains livres étroitement liés se retrouvent éloignés les uns des autres sur l’étagère, mais vous pouvez toujours les ordonner de manière à minimiser ces occurrences. C’est ce que font les algorithmes de réduction de la dimensionnalité.
Supposons que je vous donne les coordonnées GPS de tous les magasins de Palo Alto, en Californie, et que vous en traciez quelques-uns sur une feuille de papier :

Vous pouvez probablement dire juste en regardant ce tracé que la rue principale de Palo Alto va du sud-ouest au nord-est. Vous n’avez pas dessiné de rue, mais vous pouvez en déduire qu’elle se trouve là du fait que tous les points se situent le long d’une ligne droite (ou à proximité – ils peuvent se trouver de différents côtés de la rue). En effet, la rue est University Avenue, et si vous voulez faire du shopping ou déjeuner à Palo Alto, c’est l’endroit où aller. En prime, une fois que vous savez que les magasins se trouvent sur University Avenue, vous n’avez pas besoin de deux chiffres pour les localiser, mais d’un seul : le numéro dans la rue.
Si vous tracez d’autres magasins, vous remarquerez probablement que certains se trouvent sur des rues transversales, un peu à l’écart de University Avenue, et quelques-uns sont entièrement ailleurs :

Néanmoins, il n’en reste pas moins que la plupart des magasins sont assez proches de l’avenue University, et si vous n’aviez droit qu’à un seul chiffre pour localiser un magasin, sa distance par rapport à la station Caltrain le long de l’avenue serait un assez bon choix : après avoir parcouru cette distance, il suffit probablement de regarder autour de soi pour trouver le magasin. Vous venez donc de réduire la dimensionnalité de « l’emplacement des magasins à Palo Alto » de deux à un.
Par conséquent, Robby, si vous n’autorisez qu’une seule coordonnée sur sa carte de Palo Alto, a besoin d’un algorithme pour « découvrir » University Avenue à partir des coordonnées GPS des magasins. La clé est de remarquer que, si vous placez l’origine du plan x,y à la moyenne des emplacements des magasins et que vous faites lentement tourner les axes, les magasins sont les plus proches de l’axe x lorsque vous l’avez tourné d’environ 60 degrés, c’est-à-dire lorsqu’il est aligné avec University Avenue :
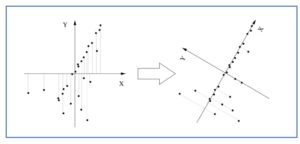
Cette direction – connue sous le nom de première composante principale des données – est également la direction le long de laquelle la dispersion des données est la plus grande. Après avoir trouvé la première composante principale, vous pouvez chercher la seconde, qui dans ce cas est la direction de la plus grande variation à angle droit par rapport à University Avenue. Sur la carte, il n’y a qu’une seule direction possible à gauche (la direction des rues transversales).
Nous pouvons appliquer la même idée à des données en milliers ou millions de dimensions, comme les images de visages, en recherchant successivement les directions de plus grande variation de sorte que la variabilité restante soit faible, moment auquel nous pouvons nous arrêter. Par exemple, après avoir fait pivoter les axes dans la figure ci-dessus, la plupart des magasins ont y = 0. La moyenne de y est donc très faible et nous ne perdons pas trop d’informations en ignorant complètement la coordonnée y. Il s’avère que l’ensemble du processus de recherche des composantes principales peut être réalisé en une seule fois avec un peu d’algèbre. Mieux encore, quelques dimensions représentent souvent la majeure partie de la variation, même dans des données à très haute dimension. Même si ce n’est pas le cas, le fait d’observer les données dans les deux ou trois premières dimensions permet souvent d’en savoir beaucoup plus, car cela permet d’exploiter les incroyables pouvoirs de perception de votre système visuel.
L’analyse en composantes principales (ACP), comme on appelle ce processus, est l’un des outils clés de la boîte à outils du scientifique. On pourrait dire que l’ACP est à l’apprentissage non supervisé ce que la régression linéaire est à la variété supervisée. La célèbre courbe en crosse de hockey du réchauffement climatique, par exemple, est le résultat de la recherche de la composante principale de diverses séries de données liées à la température (cercles d’arbres, carottes de glace, etc.) et de la supposition qu’il s’agit de la température. Les biologistes utilisent l’ACP pour résumer les niveaux d’expression de milliers de gènes différents en quelques voies. Les psychologues ont découvert que la personnalité se résume à cinq dimensions – extraversion, agréabilité, conscience, névrose et ouverture d’esprit – qu’ils peuvent déduire de vos tweets et de vos articles de blog. L’application de l’ACP aux votes du Congrès et aux données des sondages montre que, contrairement à la croyance populaire, la politique ne concerne pas principalement les progressistes contre les conservateurs. Les gens diffèrent plutôt selon deux dimensions principales : une pour les questions économiques et une pour les questions sociales. Le fait de les regrouper en un seul axe mélange les populistes et les libertaires, qui sont des opposés polaires, et crée l’illusion d’une multitude de modérés au milieu. Essayer de les séduire est une stratégie gagnante peu probable. D’un autre côté, si les progressistes et les libertaires surmontaient leur aversion mutuelle, ils pourraient s’allier sur les questions sociales, où tous deux favorisent la liberté individuelle.
Quand il sera grand, Robby pourra utiliser une variante de l’ACP pour résoudre le problème des « cocktails », qui consiste à distinguer les voix individuelles dans le brouhaha de la foule. Une méthode connexe peut l’aider à apprendre à lire. Si chaque mot est une dimension, alors un texte est un point dans l’espace des mots, et les directions principales de cet espace s’avèrent être des éléments de sens. Par exemple, le président Obama et la Maison Blanche sont éloignés dans l’espace des mots mais proches dans l’espace du sens, car ils ont tendance à apparaître dans des contextes similaires. Croyez-le ou non, il suffit de ce type d’analyse pour que les ordinateurs puissent noter les dissertations du SAT [le bac étatsunien] aussi bien que les humains. Netflix utilise une idée similaire. Au lieu de se contenter de recommander des films que les utilisateurs ayant des goûts similaires ont aimés, il projette d’abord les utilisateurs et les films dans un « espace de goût » de dimension inférieure et recommande un film s’il est proche de vous dans cet espace. De cette façon, il peut trouver pour vous des films que vous n’auriez jamais pensé aimer.
Plus difficile pour un visage
Vous seriez cependant assez déçu si vous regardiez les composantes principales d’un ensemble de données de visage. Il ne s’agit pas de ce que vous attendez, comme des expressions ou des caractéristiques faciales, mais plutôt de visages fantômes, flous au point d’être méconnaissables. Cela s’explique par le fait que l’ACP est un algorithme linéaire, et que les composantes principales ne peuvent être que des moyennes pondérées pixel par pixel de visages réels. (Aussi connus sous le nom de visages propres parce qu’ils sont des vecteurs propres de la matrice de covariance centrée des données – mais je m’égare). Pour vraiment comprendre les visages, et la plupart des formes dans le monde, nous avons besoin d’autre chose : la réduction non linéaire de la dimensionnalité.
Supposons que nous fassions un zoom arrière à partir de Palo Alto, et que je vous donne les coordonnées GPS des principales villes de la région de la baie de San Francisco :
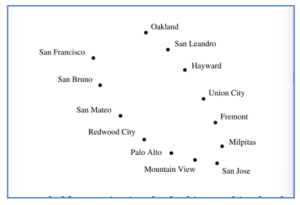
Là encore, vous pouvez probablement supposer, rien qu’en regardant ce graphique, que les villes se trouvent sur une baie [ou autour d’une montagne], et si vous tracez une ligne qui les traverse, vous pouvez localiser chaque ville en utilisant un seul chiffre : la distance qui la sépare de San Francisco le long de cette ligne. Mais l’ACP ne parvient pas à trouver cette courbe ; au lieu de cela, elle trace une ligne droite passant par le milieu de la baie, où il n’y a aucune ville. Loin d’élucider la forme des données, l’ACP l’obscurcit.
Au lieu de cela, imaginez un instant que nous allons développer la Bay Area à partir de zéro. Nous avons décidé de l’emplacement de chaque ville, et notre budget nous permet de construire une seule route les reliant. Naturellement, nous traçons une route qui va de San Francisco à San Bruno, de là à San Mateo, et ainsi de suite jusqu’à Oakland. Cette route est une assez bonne représentation unidimensionnelle de la Bay Area et elle peut être trouvée par un algorithme simple : construire une route entre chaque paire de villes proches. Bien sûr, en général, cela donnera un réseau de routes, et non une route unique passant par chaque ville. Mais nous pouvons forcer ce dernier en construisant la route unique qui se rapproche le plus du réseau, dans le sens où les distances entre les villes le long de cette route sont aussi proches que possible des distances le long du réseau.
L’un des algorithmes les plus populaires de réduction non linéaire de la dimensionnalité, appelé Isomap, fait exactement cela. Il relie chaque point de données dans un espace à haute dimension (un visage, par exemple) à tous les points proches (visages très similaires), calcule les distances les plus courtes entre toutes les paires de points le long du réseau résultant et trouve les coordonnées réduites qui se rapprochent le plus de ces distances. Contrairement à l’ACP, les coordonnées des visages dans cet espace sont souvent très significatives : l’une peut représenter la direction dans laquelle le visage est tourné (profil gauche, de trois quarts, de face, etc.) ; une autre l’apparence du visage (très triste, un peu triste, neutre, heureux, très heureux, etc.) ; et ainsi de suite. De la compréhension du mouvement dans une vidéo à la détection des émotions dans un discours, Isomap a une capacité surprenante à se concentrer sur les dimensions les plus importantes de données complexes.
Note de Vox-Fi : L’excellent site Science étonnante donne par vidéo une explication absolument limpide de la façon dont l’IA procède pour faire de la traduction automatique.
Voir : Comment les IA comprennent-elles notre langue ? Le traitement du langage naturel.
Cet article a été initialement publié sur Vox-Fi le 2 septembre 2022.







