Napoléon et Arlequin / Napoléon and Harlequin
Deux mathématisations différentes du risque financier se partagent les modélisations de la finance et s’opposent dans les représentations du monde qu’elles impliquent. L’article “Deux mathématisations de la finance : Napoléon et Arlequin”, que j’ai publié dans Les cahiers du chiffre et du droit n°3 (décembre 2015) présente de manière simple et intuitive ces deux courants de mathématisation.
Ces deux représentations différentes du risque trouvent leur origine dans les deux lois des erreurs de Laplace, présentées dans le Mémoire sur la probabilité des causes par les évènements (1774) et le Mémoire sur les probabilités (1778).
Je cherche à établir la proximité de la première loi avec les marchés réels, et l’idéologie de la seconde loi face à ces mêmes marchés. Cette comparaison me conduit à conjecturer les dangers d’une régulation financière qui évacuerait toute prise en compte de la rugosité des marchés, c’est-à-dire des critères de fragilité financière. L’article s’appuie sur la présentation technique de ces deux lois que j’ai faite dans Risques financiers extrêmes et allocation d’actifs, en particulier le tableau comparatif des univers de pensée des deux lois, à la page 138.
EN BREF
1) Qu’est-ce qui distingue ces deux lois ?
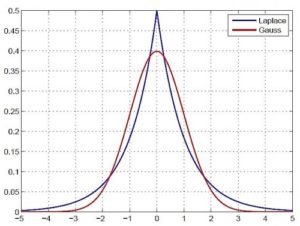
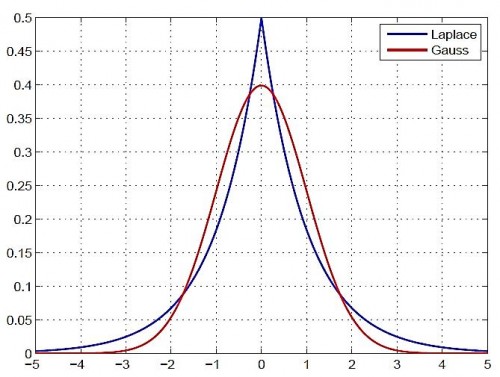
- La première loi des erreurs de Laplace (1774) privilégie les discontinuités et affaiblit la pertinence des moyennes dans la saisie des phénomènes, tandis que la seconde loi des erreurs (1778 ou loi de Laplace-Gauss) privilégie la continuité et fonde en raison le règne des moyennes et de leur corollaire l’écart type.
- La seconde loi donne l’illusion de pouvoir contrôler le risque financier et fait de la « volatilité » boursière un enjeu de régulation financière. La première loi interdit cette illusion et permet d’introduire la notion de « rugosité » d’un marché qui résiste à l’idée d’un contrôle absolu du risque par la volatilité.
2) Pourquoi Napoléon et Arlequin ?
Les professionnels du monde financier raisonnent en général en ayant à l’esprit des images mentales, des représentations du risque. Ces images qu’ils ont “dans la tête” viennent comme coiffer leurs prises de décision et leurs actions concrètes. Elles chapeautent leurs idées.
Les deux mathématisations s’apparentent à deux coiffes (deux chapeaux) pour les idées. Ces deux coiffes ressemblent aux deux formes des chapeaux de Napoléon (la gaussienne) et d’Arlequin (la première loi). Pour quelle raison ?
Au théâtre, Arlequin est un personnage vêtu d’un costume de toutes les couleurs, au chapeau pointu à bords larges. Une forme d’accent circonflexe. Le chapeau d’Arlequin ressemble mais se distingue d’un autre chapeau célèbre, le chapeau de Napoléon, moins pointu et à bords courts. Visuellement, ces deux chapeaux peuvent symboliser deux formes de loi de probabilité : l’accent circonflexe d’Arlequin pour la première loi de Laplace (celle de 1774), et la cloche du chapeau de Napoléon pour la seconde loi de Laplace (celle de 1778).
Autrement dit, on a le choix entre vouloir être habité (en pensées) par Napoléon ou par Arlequin !
Cet article a d’abord été publié dans http://epistemofinance.hypotheses.org/1516