« J’achète ce qui existe et ce qui va venir » : et si le raisonnement était valide en évaluation d’entreprise ?

Dans un article récent de la lettre Vernimmen, son auteur critique fortement le raisonnement qui consiste à dire que la valeur de la société s’obtient en ajoutant à l’existant évalué en valeur comptable des capitaux propres, la valeur actuelle des flux de trésorerie futurs de l’activité que l’on détermine par l’application d’un multiple d’EBE. Cette approche se résumerait pour l’acquéreur à « acheter ce qui existe et ce qui va venir », c’est-à-dire à faire un double compte. On montre ici que cette approche est cependant valide à condition de prendre la mesure correcte du « ce qui va venir ».
En effet, le raisonnement est parfaitement valide si au stock d’actifs initial (évalué au coût de remplacement et non simplement en montant comptable), on ajoute la somme de la valeur actuelle nette des investissements futurs de croissance. Nous montrerons dans cet article que cette méthode est équivalente à une évaluation par actualisation des flux de trésorerie (DCF).
Il faut souligner que cette modélisation de la valeur d’entreprise est très ancienne puisque présentée dès 1961 par Modigliani & Miller dans leur article séminal « Dividend Policy, Growth and the Valuation of Shares », Journal of Business 34, No 4 (October 1961), pp 411-433 [lien vers l’article]. On parle alors d’une approche d’évaluation par les opportunités d’investissement, un thème déjà évoqué par Vox-Fi.
S’inspirant des articles précédemment cités, le présent article se propose également de présenter quelques enseignements pratiques à tirer d’une modélisation de la valeur de l’entreprise par l’approche par « les opportunités d’investissement » ou « options de croissance ». Ainsi, nous partons du modèle d’actualisation d’une rente perpétuelle à croissance constante, modèle fréquemment utilisé en évaluation d’entreprise par exemple pour calculer la valeur terminale dans une évaluation par la méthode DCF.
Pour ce faire, plutôt que de recourir à l’algèbre qui pourrait décourager à bien des égards plusieurs de nos lecteurs, nous partirons d’un exemple numérique pour aboutir à une dérivation de la formule d’évaluation des opportunités d’investissement en prenant le soin de souligner les hypothèses implicites de la modélisation.
Soit l’entreprise Croissance+ qui présente un coût du capital de 15 % et dont l’actif économique, d’une valeur comptable de 75 M€, dégage une rentabilité économique de 20 %. L’activité génère donc un résultat d’exploitation de 15 M€. Par ailleurs, l’entreprise investit dans son stock d’actifs fixes et circulants (CAPEX et variation du BFR) une part fixe, disons la moitié de son résultat d’exploitation. Il y a donc 7,5 M€ d’investissements nets ou investissements de croissance. Disant cela, on suppose implicitement que les investissements de maintien correspondent aux dotations d’amortissements. Il vient donc que le flux de trésorerie disponible pour ses bailleurs de fonds s’établit à 7,5 M€.
Il faut souligner qu’en considérant des investissements de croissance proportionnels au résultat d’exploitation et que ceux-ci dégagent une rentabilité marginale égale au taux de rentabilité économique, nous faisons l’hypothèse d’une croissance stable du résultat d’exploitation. Suivant ces hypothèses, le taux de croissance à long terme est de 10 %.
On obtient en appliquant la formule de la rente perpétuelle croissante, une valeur de l’actif économique égale à :
![]()
Si l’on suppose qu’un investisseur souhaite acquérir uniquement le droit de percevoir les flux de trésorerie disponibles dégagés par le stock d’actifs détenus aujourd’hui et sans investir au-delà de ce qui est nécessaire pour maintenir son rendement actuel, il suffira qu’il paie la somme suivante qui correspond à la valeur des actifs en place :
![]()
Notre investisseur, ayant acquis l’actif économique pour 100 M€, se rend compte qu’il pourrait finalement développer le patrimoine de l’entreprise, en investissant au terme de la première année une fraction des résultats d’exploitation. Ce taux de réinvestissement des résultats d’exploitation, soit k est fixe, ici égal à 1/2 :
![]()
La valeur actuelle nette de cet investissement en fin de période 1 est :
![]()
En période 2, il pourra investir :
![]()
Il faut noter l’hypothèse de la stabilité de la rentabilité marginale du capital à chaque génération d’investissement. Ainsi, la valeur actuelle nette de chaque génération de capital croît d’un facteur constant (1+g), soit 10 % par an.
![]()
Il en va de même pour l’investissement en période 3, 4, etc. On peut donc conclure que l’investisseur en acquérant le droit de détention du stock initial d’actif économique, acquiert également des tickets d’investissements dont la valeur totale correspond à la somme des valeurs nettes des investissements de croissance futurs actualisées à la date d’acquisition. Il est évident que sur des marchés concurrentiels, aucun investisseur ne sera incité à céder un actif économique à un prix n’intégrant pas la valeur de ces tickets d’investissements futurs.
Le total des options de croissance NPV1, NPV2, NPV3, etc., correctement actualisées, est donc :
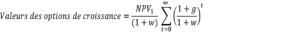
Cette équation n’admet de valeur finie que dans le cadre où le taux de croissance (g) est inférieur au coût du capital (w). Nous reviendrons plus longuement sur ce point dans la suite de cet article.
Après développement, on obtient :
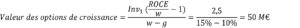
Pour résumer, on peut écrire :
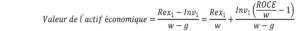
Par ailleurs, notons qu’il existe un écart de 25 M€ entre la valeur de remplacement des actifs en place estimée à 100 M€ et leur valeur comptable (A0) de 75 M€. Cette différence correspond à la valeur actuelle des profits économiques générés par le stock d’actifs initial :
![]()
En effet, la valeur de remplacement des actifs en place est égale à la valeur d’échange de ces actifs sur un marché concurrentiel. Sachant qu’il y a un profit économique à la clé, cette valeur n’est pas de 75 M€ mais de 75 + 25 = 100 M€.
Pour finir, on retrouve le raisonnement qui veut que « l’on achète ce qui existe et ce qui va venir ».
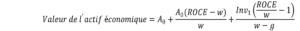
Rendu à ce point, l’erreur de double comptage souligné au début de cet article devient évidente : il est erroné de considérer que la valeur de l’actif économique obtenue par application d’un multiple de l’EBE ne représente que la valeur actuelle des flux de trésorerie futurs que l’activité dégagera. Elle intègre également la valeur comptable de l’actif économique dont la détention permettra la création de ces richesses futures au travers d’investissements de croissance.
Ce premier point étant clarifié, il convient de tirer des enseignements pratiques de cette modélisation de la valeur des options de croissance.
1) La croissance ne se décrète pas !
Il est facile avec le développement des tableurs de faire des prévisions en affectant un taux de croissance arbitraire au chiffre d’affaires sans s’assurer de la cohérence de cette croissance avec la taille de l’actif économique. Par ailleurs et il faut le rappeler, la croissance doit être financée, soit par rétention de dividendes, soit par augmentation de capital ou encore par endettement. Ainsi, il ne suffit pas en modélisation financière de rentrer les bonnes formules dans Excel et de s’assurer que le bilan s’équilibre, pour avoir un modèle financier correct.
2) Les arbres ne montent pas jusqu’aux cieux !
Utiliser un modèle de rentes perpétuelles à croissance constante pour évaluer la valeur terminale dans un modèle financier revient à faire l’hypothèse implicite que l’entreprise dégagera à perpétuité une rentabilité marginale sur ses investissements futurs en excédent de son coût du capital. Comme un auteur français en finance d’entreprise bien connu aime à le dire : « il n’y a pas de forteresses imprenables, juste des citadelles mal attaquées. » Il est sage de toujours garder à l’esprit la difficulté de dégager des superprofits de manière durable sans attirer sur ses marchés des compétiteurs qui tendront à tirer les marges vers le bas jusqu’au point d’équilibre. À l’équilibre, il ne sera possible que de gagner le coût du capital.
3) Et si la croissance était supérieure au coût du capital ?
En lisant le point précédent, on peut déjà la deviner. Il n’est pas possible que sur des marchés concurrentiels, on atteigne un équilibre où il serait possible à perpétuité de réinvestir une proportion constante de ses résultats dans un actif générant une rentabilité en excès du coût du capital. Il faut se rappeler que le coût du capital n’est pas figé comme dans notre modèle, où il est considéré comme une variable exogène. Au contraire, il s’ajuste au fil du temps à la demande et à l’offre de capitaux.
De manière plus intuitive, le taux de croissance g doit être nécessairement inférieur au coût du capital car il n’est pas possible sur des marchés compétitifs d’acheter ou de vendre le droit de percevoir des flux de trésorerie infinis pour un montant fini. En gros, personne n’acceptera d’échanger pour un montant fini, un contrat qui lui donne le droit potentiellement de détenir tous les actifs de l’univers. L’image est un peu forcée, soit ! Mais elle traduit bien le principe.
4) Et si la valeur des options de croissance était négative ?
Une valeur négative des options de croissance est loin d’être contre-intuitive. Au contraire, elle s’explique fort bien. En effet, elle matérialise simplement le fait qui si les investissements marginaux futurs sont acquis systématiquement à des prix excédant la valeur actuelle des revenus que l’on peut attendre de la détention de ces actifs, la firme détruira de la valeur. Il ne suffit pas de croître pour créer de la valeur !
Par ailleurs, une valeur négative des options de croissance (VAOC < 0) explique pourquoi certains titres ont un ratio Price-to-Book (PBR) inférieur à l’unité. En effet, les entreprises ayant structurellement ce niveau de ratio (secteur bancaire par exemple) détruisent de la valeur car elles dégagent une rentabilité inférieure au coût du capital.
Cela ne peut pas durer à long terme sans que l’on s’expose à des faillites et/ou à des restructurations massives. L’actualité récente dans le secteur bancaire en est une parfaite illustration.
Découvrez d'autres articles










